Help
| IDENTIFY FUSION NETWORK | TOPOLOGICAL CONCEPTS OF PPI NETWORKS |
Objective: Identify Fusion Network
Step 1: Enter Protein Name(s)
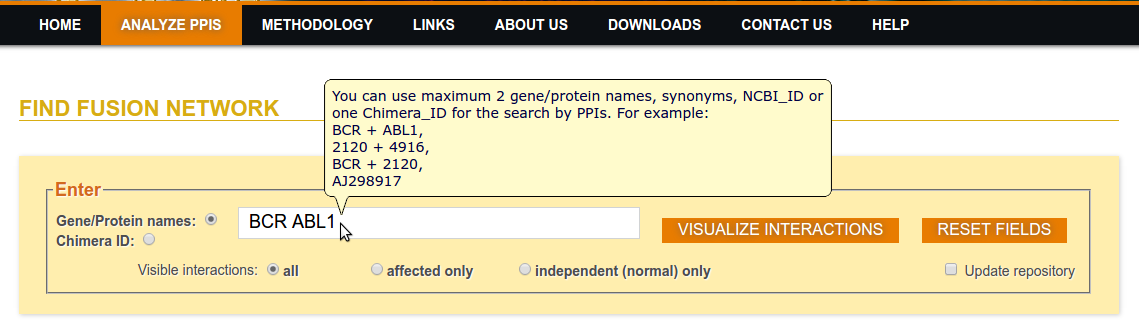
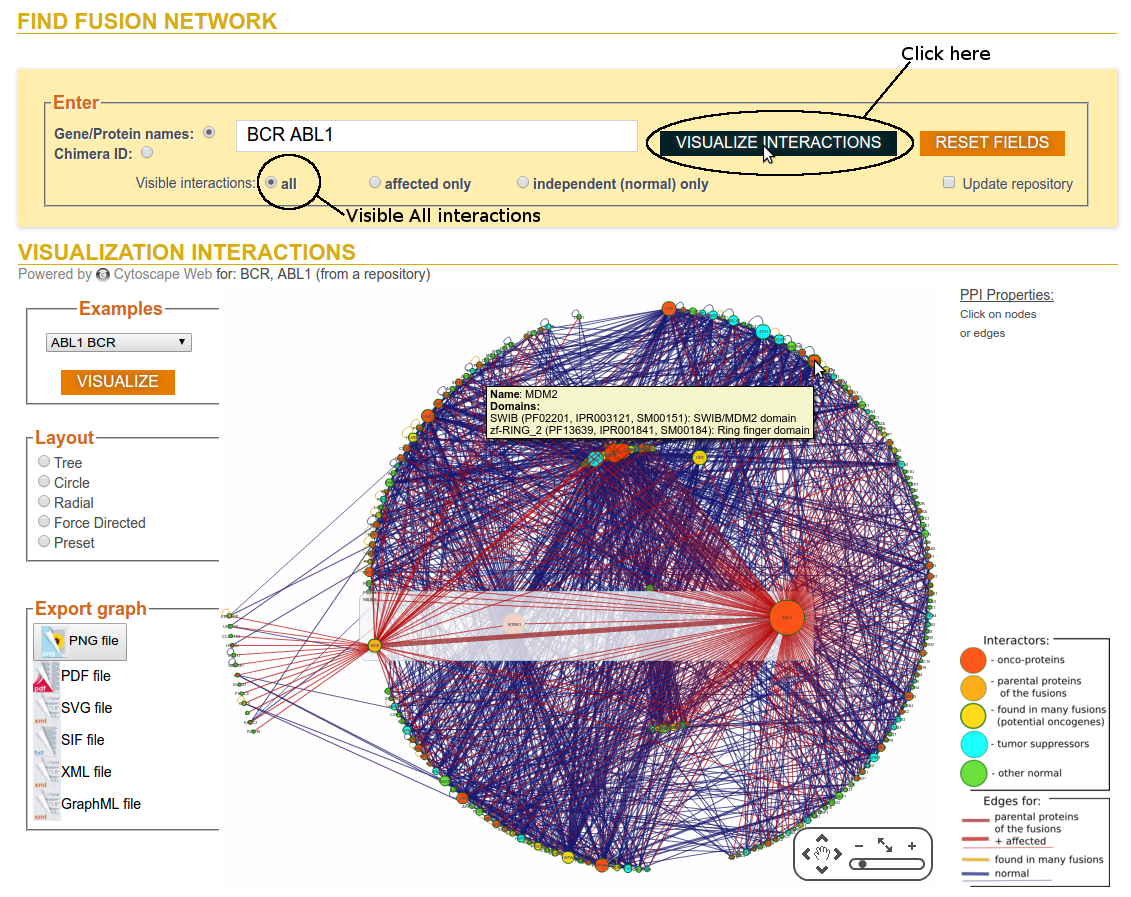
Step 2a: Click on Visualize Interactions (Visible All interactions)
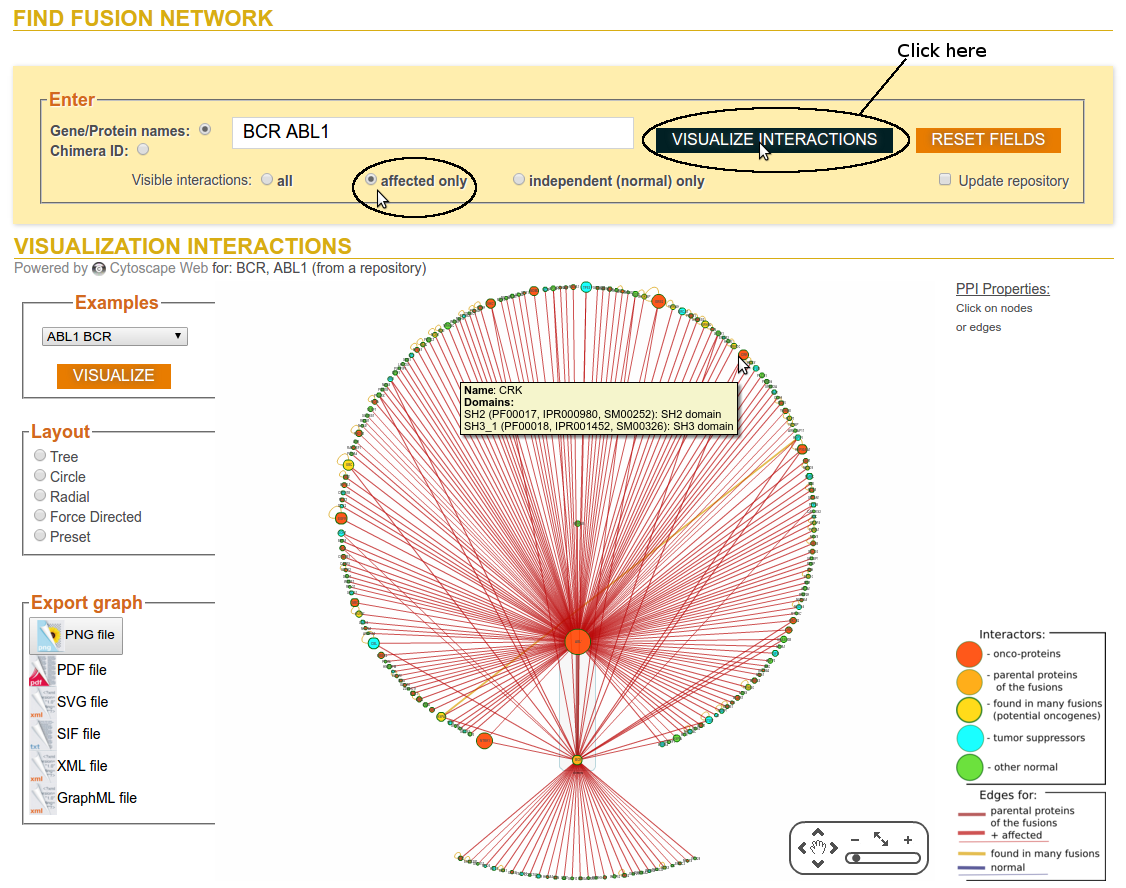
Step 2b: Click on Visualize Interactions (Visible affected interactions only)
Step 3a: Visualization Options (Click on node of interest)
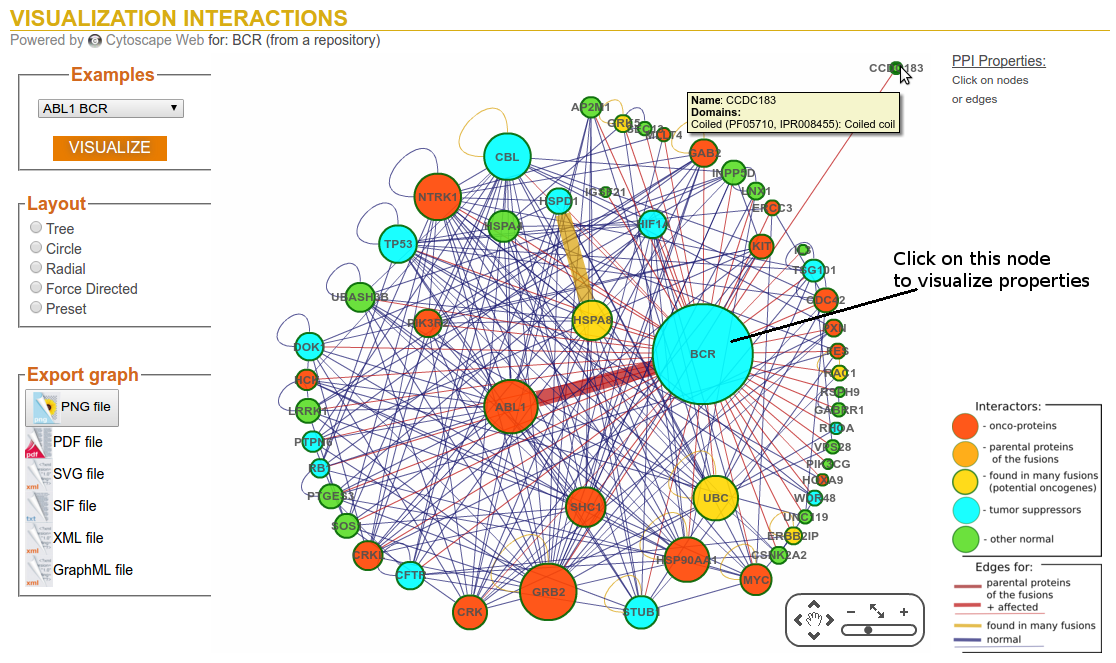
Step 3b: Visualization Options (PPI Properties)
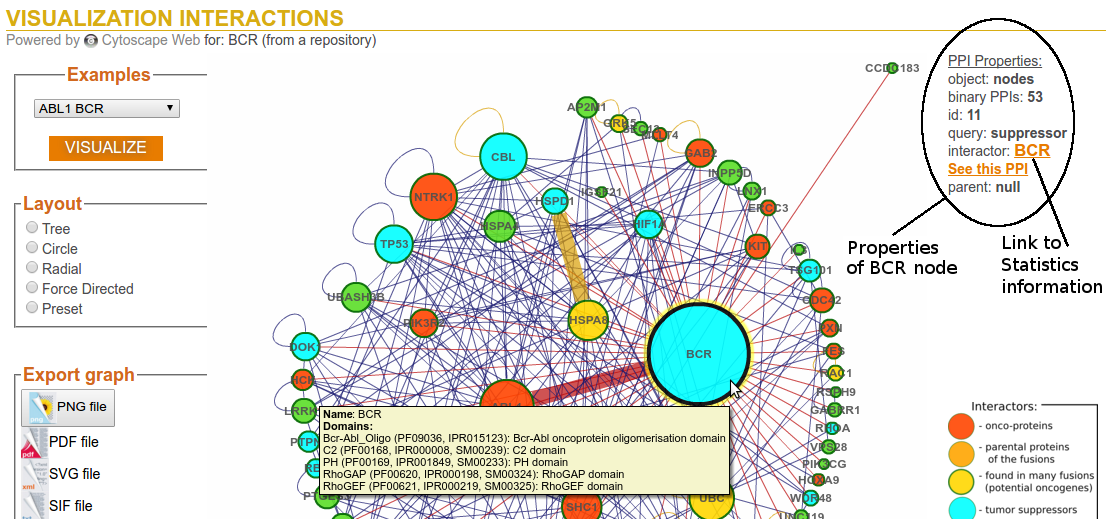
Step 3c: Visualization Options (Layout - Tree)
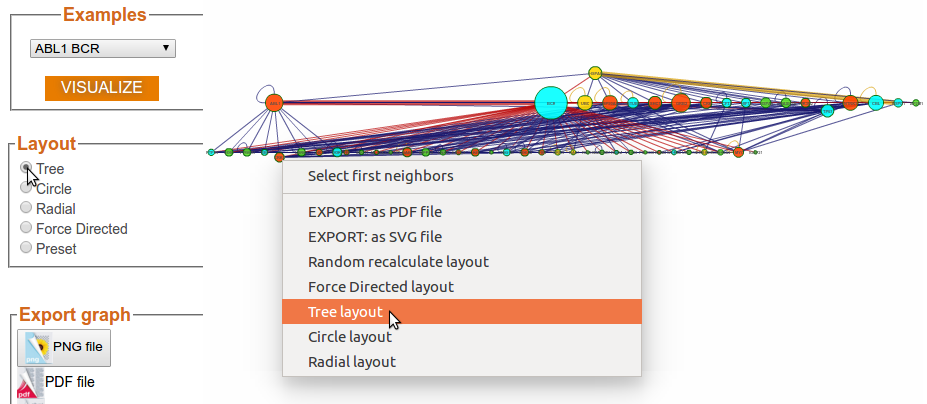
Step 3d: Visualization Options (Layout - Circle)
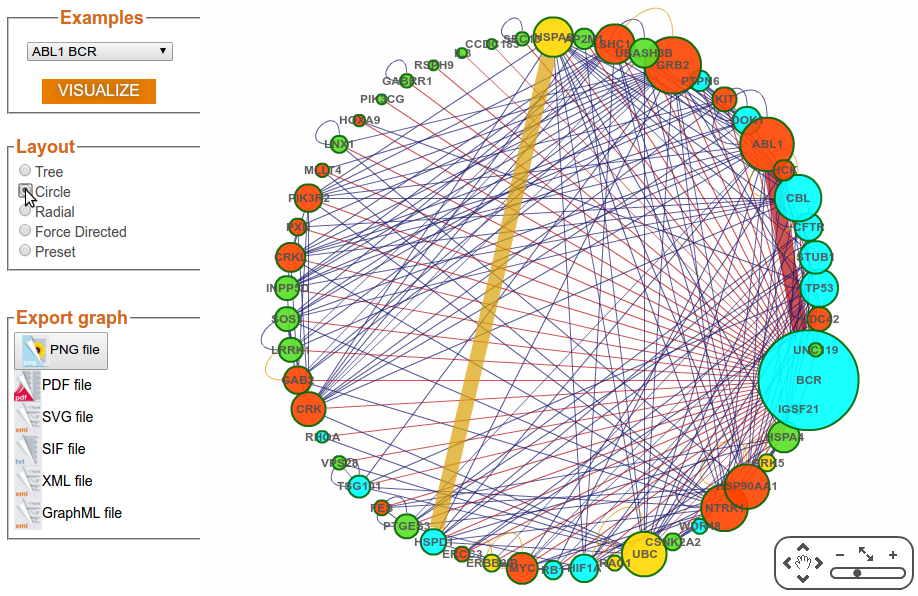
Step 3e: Visualization Options (Layout - Radial)
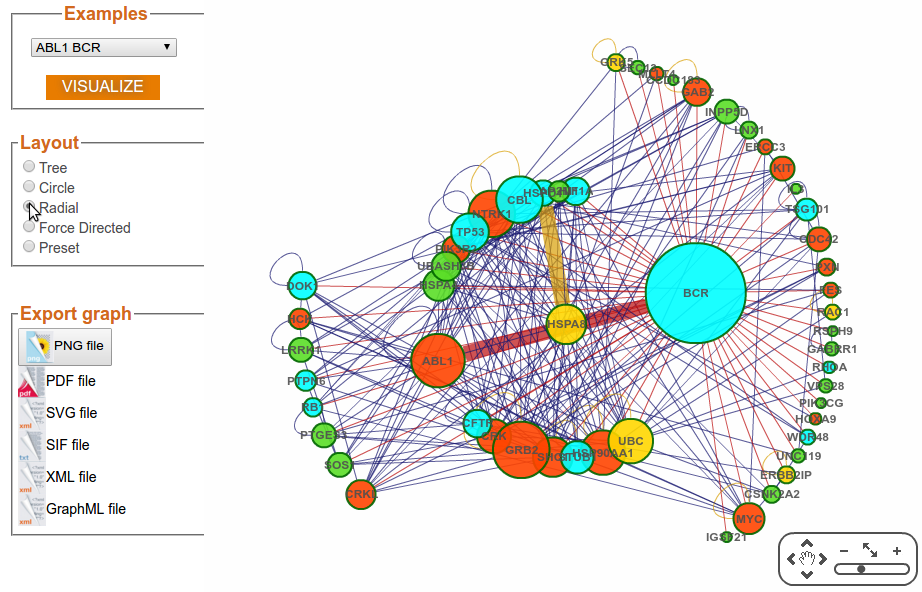
Step 3f: Visualization Options (Layout – Force Directed)
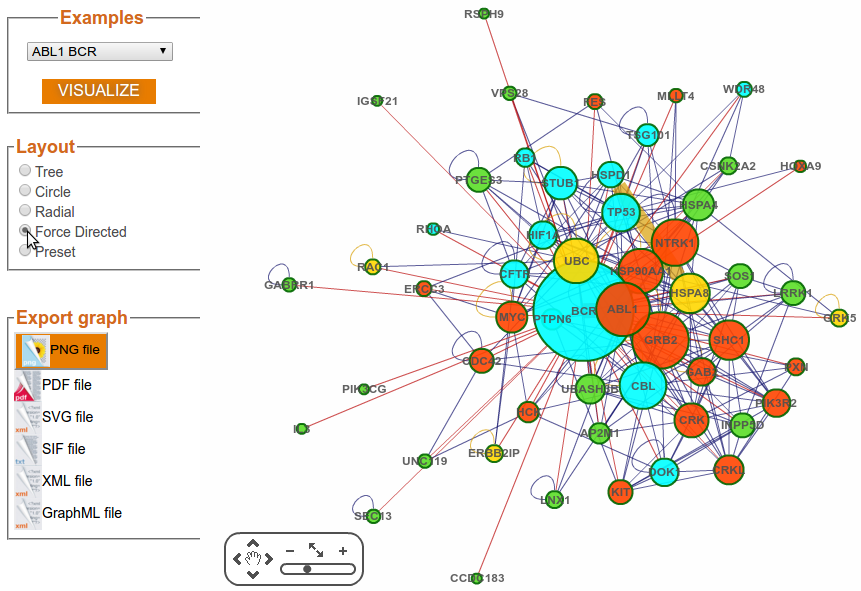
Step 4: Export map
The graphical output is produced in PNG, PDF, and SVG format.
Downloading the figure in SVG format will allow you to further customise it with SVG compatible
software such as for instance InkScape (which is freeware
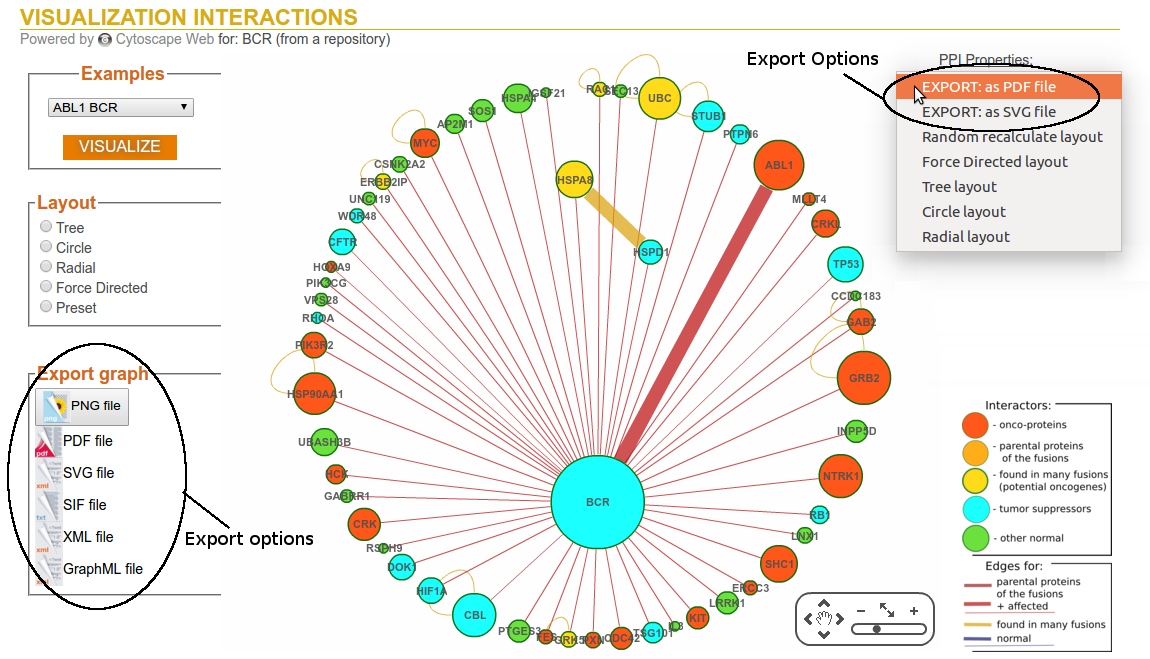
Step 5: Statistics Information
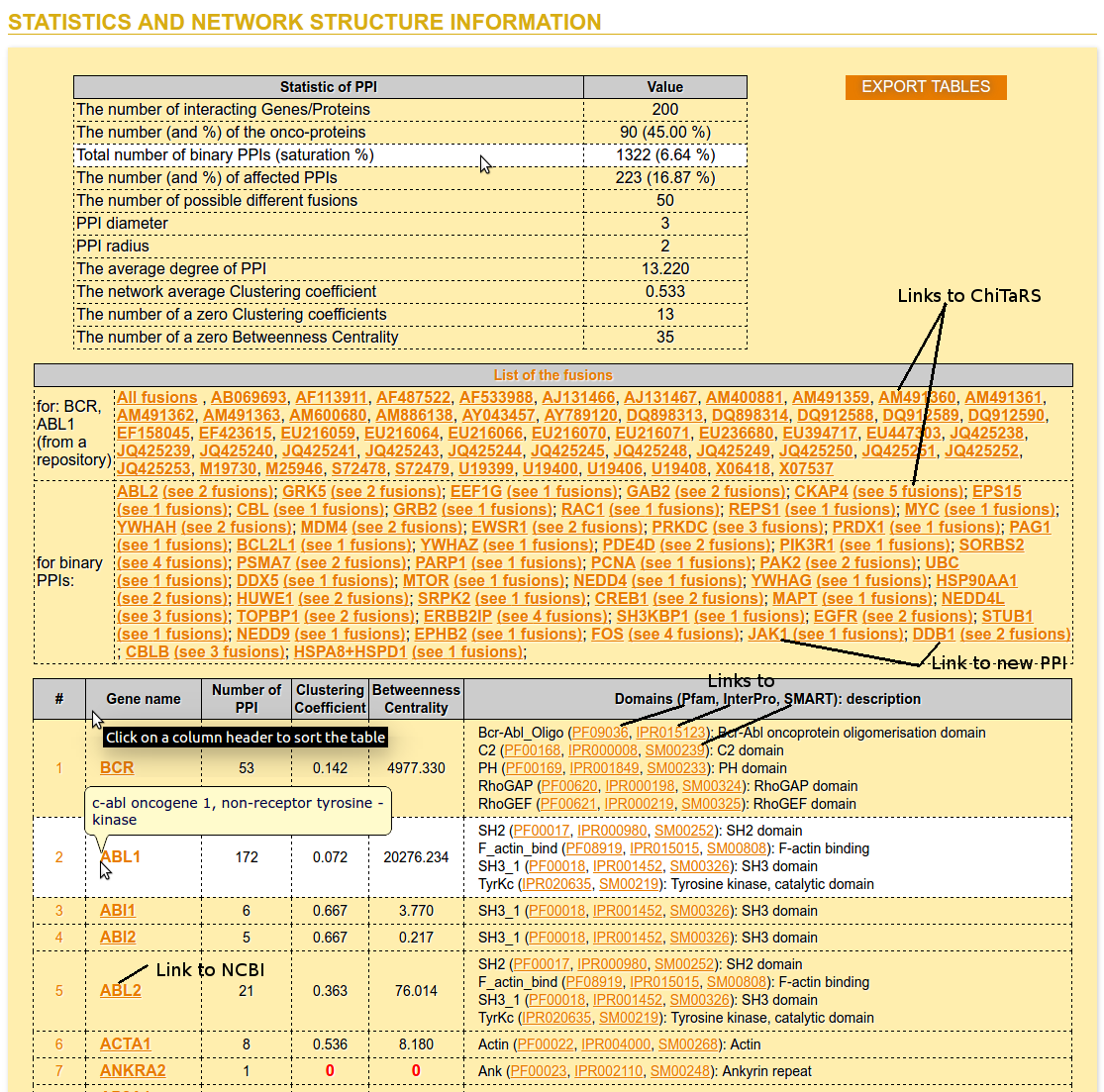
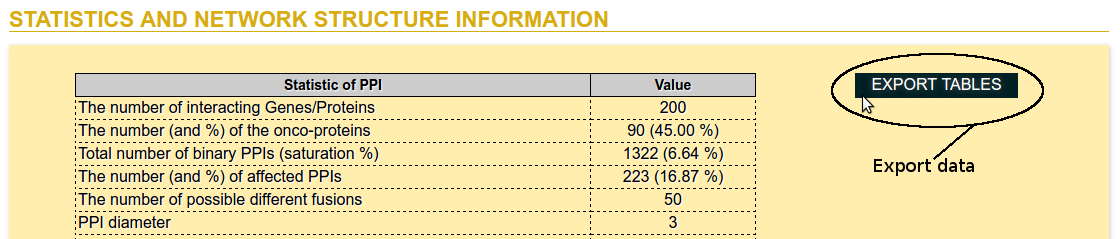
Step 6: Export data
TOPOLOGICAL CONCEPTS OF PPI NETWORKS
In this section we consider the protein-protein interaction (PPI) network as a graph: G = (V, E) in which V and E are vertex set and edge set of the graph respectively, we also suppose that the number of vertices are n and the number of edges are e.
Some of the most important topological concepts of protein-protein interaction networks are as follows:
Degree: for a vertex v shows the number of its interactions and represent as deg(v).
Hub: nodes with high degree called hub which suggested having an important role in cellular processes.
Edge Density (ED): is the ratio of the number of network edges to the maximum possible number of edges that can be computed as equation:
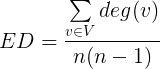
Clustering Coefficient (CC): for a vertex such as v if Ev shows the maximum number of possible interactions between neighbors of v and Fv shows the number of neighbors of v that interact with each other then clustering coefficient for v is defined as follows:
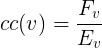
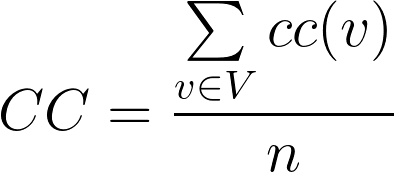
Path length: the least number of edges needed to reach from one vertex to another called the path length between them.
Average path length: the average path length over all possible vertex pairs in the network.
Diameter: the maximum path length in the network.
Centrality: in general centrality is a structural attribute of nodes or edges that shows the importance of those nodes
or edges in the network. There are many centrality measures, however, we describe three of the most popular centrality measures below:
❶Degree centrality is the simplest centrality measure, which is defined as the number of edges incidences with that node,
in the normalized version the degree is divided by the maximum possible degree.
❷Closeness centrality is based on the distance of a node to all other nodes in the graph and is precisely defined as follows:
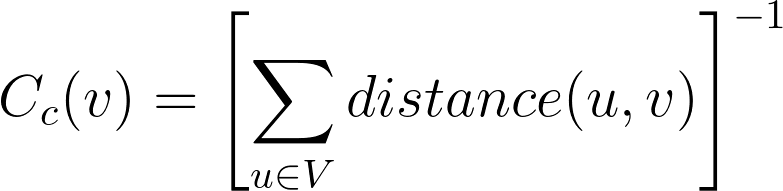
❸Betweenness centrality for a node v is defined as the number of shortest paths passing through v, this measure can be defined for an edge in the same way. A protein with high betweenness centrality value has great influence over information flows in the whole network. In spite of closeness centrality, betweenness centrality can be used for disconnected networks.